Ref:sas.upenn.edu/⁓mcnemar/apchem/nuclear.pdf
Prerequisites: Composition of atom, particularly the composition of atomic nucleus.
Nuclear Chemistry Why?
Nuclear chemistry is the subdiscipline of chemistry that is concerned with changes in the nucleus of elements. These changes are the source of radioactivity and nuclear power. Since radioactivity is associated with nuclear power generation, the concomitant disposal of radioactive waste, and some medical procedures, everyone should have a fundamental understanding of radioactivity and nuclear transformations in order to evaluate and discuss these issues intelligently and objectively.
Learning Objectives
- Identify how the concentration of radioactive material changes with time.
- Determine nuclear binding energies and the amount of energy released in a nuclear reaction.
Success Criteria
- Determine the amount of radioactive material remaining after some period of time.
- Correctly use the relationship between energy and mass to calculate nuclear binding energies and the energy released in nuclear reactions.
Resources
- Chemistry Matter and Change pp. 804-834
- Chemistry the Central Science p 831-859
Prerequisites
Atoms and isotopes
New Concepts
nuclide, nucleon, radioactivity, α− β− γ−radiation, nuclear reaction equation, daughter nucleus, electron capture, positron, fission, fusion, rate of decay, decay constant, half-life, carbon-14 dating, nuclear binding energy
Radioactivity
Nucleons: two subatomic particles that reside in the nucleus known as protons and neutrons Isotopes Differ in number of neutrons only. They are distinguished by their mass numbers. 23392U Is Uranium with an atomic mass of 233 and atomic number of 92. The number of neutrons is found by subtraction of the two numbers nuclide applies to a nucleus with a specified number of protons and neutrons. Nuclei that are radioactive are radionuclides and the atoms containing these nuclei are radioisotopes.
Nuclear equations
Some atoms are unstable. Emission of particles or electromagnetic radiation is one way to gain stability.
Alpha radiation
Uranium-238 undergoes alpha decay in attempt to be stable: 238 92U → 234 90Th + 4 2He
Alpha particle is the nucleus of He (alpha = α = 42He)
Daughter nuclide: the nuclide formed from the decay (23490Th)
Parent nuclide: the original nuclide undergoing decay (238 92U)
Beta radiation
Consists of a stream of beta particles which are high speed electrons. Represented by the symbol 0 -1e
Iodine-131 is an example of a radioactive isotope that undergoes Beta emission. (an antineutrino also emitted): 131 53I → 131 54Xe + 0 -1e
Notice the atomic number increases. Beta emission results in the conversion of a neutron (1 0n) to a proton (1 1p): 1 0n → 1 1p + 0 -1e (the electron comes from the neutron being converted to proton, NOT from the electron cloud)
Gamma radiation
High energy photons (electromagnetic radiation of a short wavelength)
Gamma radiation does not change the mass or atomic number and is represented as 0 0γ.
It almost always accompanies other radioactive emission because it represents the energy lost when the remaining nucleons reorganize into more stable arrangements. Generally you do not show gamma rays when writing nuclear equations
Positron emission
A positron is a particle that has the same mass as an electron but opposite charge. The positron is represented as 0 1e. Carbon-11 is an example of a particle that undergoes positron emission: 11 6C → 11 5B + 0 1e
Notice the atomic number goes down. Positron emission is the effect of converting a proton to a neutron: 1 1p → 1 0n + 0 1e
Electron capture
Capture by the nucleus on an inner shell electron of the electron cloud. Rubidium-81 does this: 81 37Rb + 0-1e(orbital electron) → 81 36Kr
Electron capture has the effect of positron emission, converting a proton to a neutron: 1 1p → 10n + 0 1e
Nuclear Stability
What makes a nucleus stable? It depends on a variety of factors and no single rule allows us to predict whether a nucleus is radioactive and might decay unless we observe it. There are some observations that have been made to help us make predictions
Neutron to proton ratio
Strong nuclear force exists between nucleons. The more protons packed together the more neutrons are needed to bind the nucleus together. Atomic nucleus with an atomic number up to twenty has almost equal number of protons and neutrons. Nuclei with higher atomic numbers have more neutrons to protons. The number of neutrons needed to create a stable nucleus increase more than the number of protons.
Belt of stability
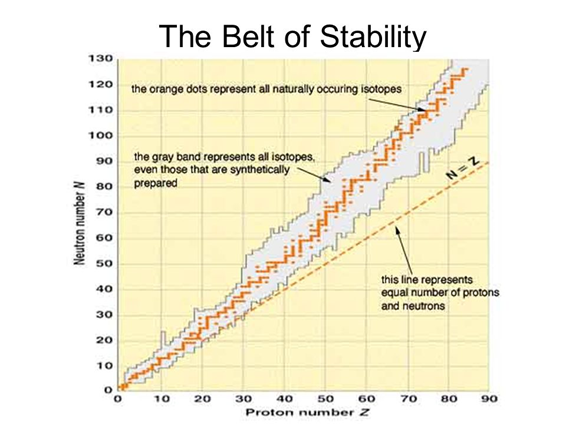
(slideplayer.com)
All nuclei with 84 or more protons are radioactive
1. Nuclei above the belt of stability. These neutron rich isotopes can lower their ratio and move to the belt of stability by emitting a beta particle. This increases number of protons and decreases neutrons
2. Nuclei below the belt of stability. These proton rich nuclei increase their neutrons and decrease protons by positron emission (more common in lighter nuclei) and electron capture (more common in heavier nuclei): 1 1p → 1 0n + 01e
3. Nuclei with atomic numbers greater than 84. These tend to undergo alpha emission. This emission decreases the number of neutrons and protons by 2 moving the nucleus diagonally toward the belt of stability: 23892U → 234 90Th + 4 2He
EXAMPLE: Predict what mode of decay will C-14 undergo?
Just remember this is a prediction and may not always go as predicted.
Radioactive series
Some nuclei will not gain stability by one emission and may undergo many until they reach stability. For example, U-238 decays to Th-234 which decays to Pa-234 which decays…eventually, lead-206 is obtained
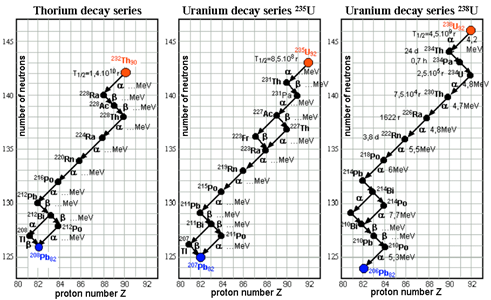
(astronuclphysics.info)
Three series occur in nature. The other two is Uraniunm-235 to lead-207 and thorium-232 and ends with lead-208
Other observations for prediction
• Nuclei with 2,8,20,28,50, or 82 protons or 2,8,20,28,50,82, or 126 neutrons are generally more stable..magic numbers
• Nuclei with even number of protons or neutrons are more stable than odd number These stability factors can be liken to the stability of 2,8,18,32 in electron shells
Nuclear Transmutations
Nuclear reactions that are induced are called nuclear transmutations. The first conversion was performed by Rutherford in 1919. Converted nitrogen-14 into oxygen-17 by bombarding with alpha particles from radium: 14 7N + 4 2He → 17 8O + 1 1H
The particles must be moving fast to overcome the electrostatic repulsion between the charged particle and the charged nucleus.
Particle accelerators (atom smashers)
Fermi National accelerator laboratory in Batavia, Ill has a particle accelerator 6.3 km in circumference
Using neutrons
Neutrons can be used to bombard nuclei and do not need to be accelerated since they have no charge. All transuranium elements (elements after uranium that are synthetic) are produced by this method: 23892U + 1 0n → 239 92U → 23992Np + 0 -1e
Some are made by bombardment of one atom type with another. Bismuth bombarded with nickel for several days produced element 111.
Rates of Radioactive Decay
Radioactivity is a first order reaction. In a first order reaction, the rate of the reaction is given by the expression: -ΔN/Δt = kN where ΔN change in the amount of the radioactive nuclide, Δt interval time, k is radioactivity constant, N amount or concentration of the radioactive nuclide.
From the expression of the rate of the reaction, arrangement can be made in integrated expression: Nt = Noe-kt where Nt = the remaining amount of the radioactive nuclide after a time t, No = the starting amount of the radioactive nuclide.
From this expression, we get: lnNt = ln (No e-kt) = lnNo + ln e-kt
lnNt - lnNo = lnNt/No = -kt (1)
Half-life time
First order reactions are characterized by their half-life time, the time required for the amount of the reactant to decrease to ½ of its initial value, No/2; it is represented by the symbol t1/2.
Equation (1) can be written as: lnNo/2No = ln1/2 = -kt1/2 or ln2 = kt1/2
From the previous expression: ln2 = 0.693 = kt1/2, or t1/2 = 0.693/k
Dating
Because the half-life of any nuclide is constant, the amount of substance remaining in an artifact can serve as a nuclear clock to determine ages of objects. When an animal is alive it maintains a carbon-14 to carbon-12 ratio identical to that in the atmosphere. When it dies, this ratio decreases. By measuring this ratio and contrast it to the atmosphere, we can get an approximate age. Radioactive decay is a first order process. Remember, half-life of a first order process is T1/2 = 0.693/k where k is the decay constant. We can determine the k constant by using the rate equation of a first order reaction
ln (Nt/No) = -kt
Example: If we start with 1.000 grams of Sr-90, 0.953 grams will remain after 2.0 years. (a) what is the half-life of strontium-90? (b) How much strontium-90 will remain after 5.00 years?
(28.8 yr, 0.887g)
Energy Changes in Nuclear Reactions
E = mc2
A very familiar equation that shows mass and energy change are proportional. If a system loses mass, it loses energy (exothermic) and if it gains mass, it gains energy (endothermic). The c2 shows a small mass loss can cause a large energy loss. This is why conservation of mass seems to hold in reactions. For example, combustion of one mole methane loses 9.9 x 10-9 grams. In nuclear reactions, this mass change are much greater, 50,000 times greater than methane combustion. Look at the following: 23892U → 234 90Th + 4 2He.
The nuclei in this reaction have the following masses: 238 92U = 238.0003 amu, 234 90Th = 233.9942 amu and 4 2He = 4.0015 amu. The m is products minus reactants is 233.9942 + 4.0015 – 238.0003 = -0.0046g. Change in energy would be E = (-0.0046 g)(1kg/1000g) (3.00 x 108 m/s)2 = -4.1 x 10 11 kg-m2 /s2 = -4.1 x 1011J
Example: How much energy is lost or gained when Co-60 undergoes beta decay? Mass of Co-60 is 59.9338 amu, Mass of Ni-60 is 59.9308 amu. (-2.7 x 1011 J)
Nuclear Binding Energies
Scientists discovered in the 1930s that the masses of nuclei combined are always less than these nucleons individually. Mass of 2 protons 2(1.00728 amu). Mass of 2 neutrons 2(1.00867 amu). Total = 4.03190 amu. The mass of a Helium-4 nucleus is 4.00150 causing a mass defect of 0.0304 amu. The origin of this mass defect is some of the mass is converted to binding energy which binds the nucleons together in the nucleus. Energy then needs to be added to separate these nucleons to overcome this binding energy. This energy added to break the nucleons apart is called nuclear binding energy
Nuclear Fission
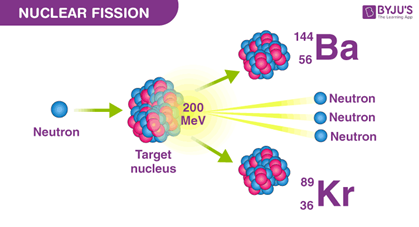
(byjus.com)
Problem: radioactive elements are used
Nuclear Fusion
D + T → 4He + n + Energy
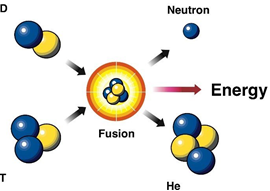
(energy.gov)
Combining of nuclei also release energy.
Uses: possible alternative energy source that can fuse light nonradioactive nuclei to obtain energy. Problem: The reaction needs high temperatures to overcome the repulsion between nuclei. . The lowest temperature found to fuse deuterium with tritium is 40,000,000 K. Cold Fusion is a hot research topic today.